X-Ray Diffraction: Getting to Know Crystal Structures (Part Ⅰ)

When we study materials, utilizing X-ray to understand crystalline structure is essential. Microscopic structure and atomic composition determine critical properties of matter such as the melting point, the viscosity, the stiffness, and more. Those are important properties for scientists to discover the function and uses of materials. X-Ray diffraction methods are the most efficient way to determine and characterize the crystalline structure of solid materials. Diffraction methods, including X-ray diffraction, electron diffraction and neutron diffraction, can identify different compounds or phases that have the same composition with their unique crystalline structure. In this and next blog post, we are going to discuss the spectroscopic technique which is also known as X-Ray powder diffractometry (XRD), the most widely used diffraction method for material characterization. 

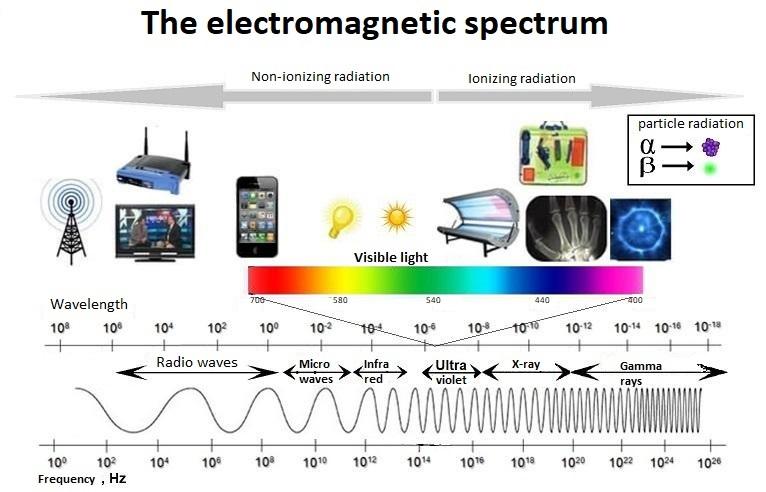
The electromagnetic spectrum gives an overview of all electromagnetic radiation. Courtesy of uib.no.

Today’s blog post is sponsored by DataRay – Advancing the technology of laser beam analysis since 1988

What is an X-ray?

An X-ray is a penetrating form of high-energy electromagnetic radiation. Most X-rays have a wavelength ranging from 10 picometers to 10 nanometers, λ= 0.01 – 10 nm (0.1 – 10 Å; 1 Å = 10^-10 m) – wavelengths that are shorter than UV rays and typically longer than gamma rays, and coincidentally about the distance between the atoms. This corresponds to frequencies in the range of 30 petahertz to 30 exahertz (30×10^15 Hz to 30×10^18 Hz) and energies in the range of 124 eV to 124 keV.

Because of their unique wavelength close to the interatomic distances, when X-rays hit an object, outgoing waves are generated, which in turn can under certain conditions, create an interference pattern due to the scattering from the different atoms. Analyzing the resulting interference patterns allows us to determine arrangement of atoms in materials.

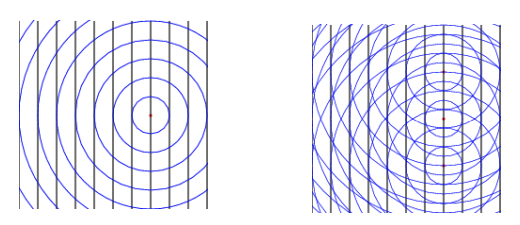
Waves scattered from different atoms (single atom / array of atoms) create interference pattern.

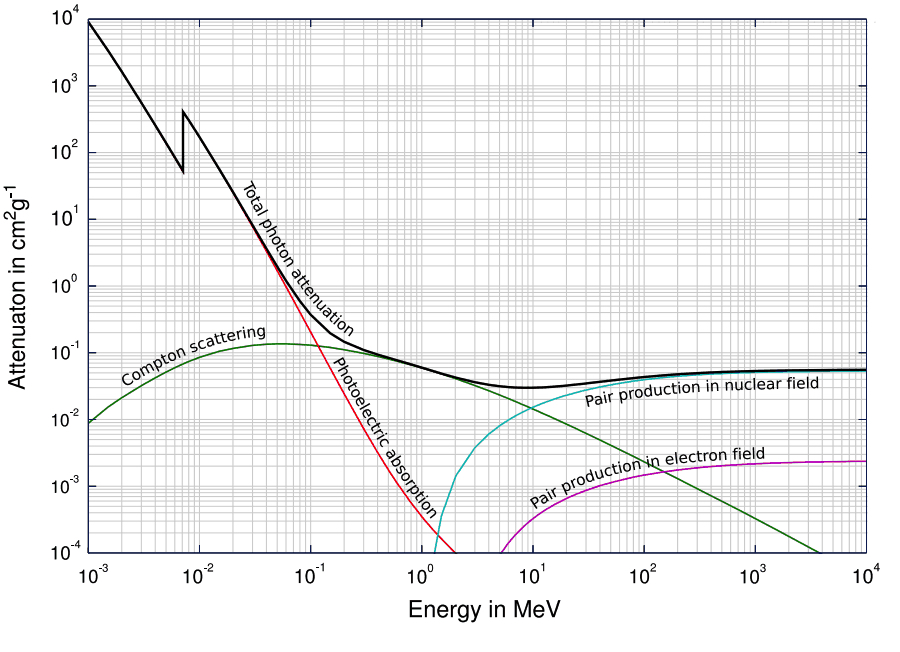
The penetrating power of X-ray is above most of the absorption energies. As we increase the photonic energy, the absorption starts dropping rapidly which means we get significant penetration power with X-rays. This is why x-rays are used in medical areas for imaging.

Total photon cross sections of X-ray attenuation. Courtesy of material-properties.org.

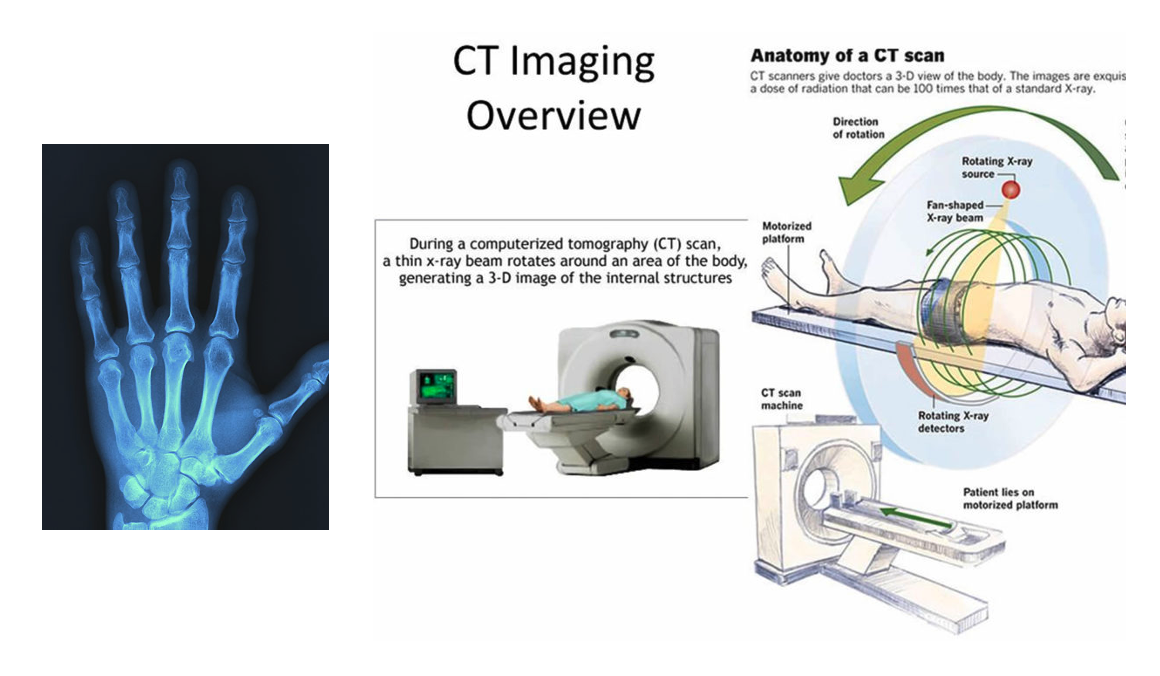
Left: 2 dimensional X-ray medical image. Courtesy of imaginghealthcare.com. Right: A computerized tomography (CT) or computerized axial tomography (CAT) scan combines data from several X-rays to produce a detailed image of structures inside the body. CT scans produce 2-dimensional images of a “slice” or section of the body, but the data can also be used to construct 3-dimensional images. Courtesy of omegapds.com.

How do we make X-rays?

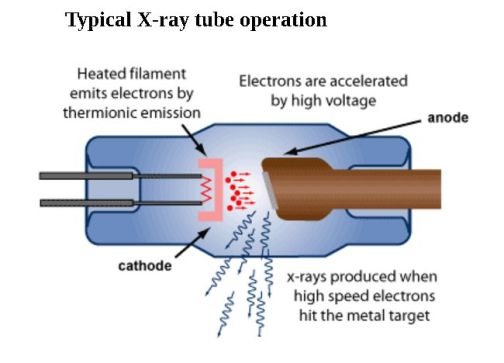
We use X-ray tubes to generate X-rays. Everything happens inside an enclosed chamber (tube) which is under vacuumed. A heated filament placed inside the tube emit electrons by thermionic emission, which are accelerated towards a target anode because of a high voltage applied between the cathode and the anode. Subsequently, X-rays are produced on the target surface and radiated in all directions. Specially placed windows help guide X-rays out of the tube in a specific direction. Interestingly, most of the kinetic energy of electrodes is converted into heat, with only ~0.99% transformed into X-rays.

X-ray Sources: Conventional Lab-Based X-ray Machines. Courtesy of designworldonline.com.

A typical X-ray spectra is characterized by a relatively continuous distribution with sharp intensity maxima overlaid at a certain wavelength. When an incident electron with sufficient energy excites an electron in the inner shell of an atom to higher energy state, the vacancy left in the inner shell will be filled by an electron in an outer shell. During this process, this electron would release energy by emitting an X-ray with a specific wavelength of photons with specific energy. For example, if a K shell vacancy is filled by an electron from  the L shell or M shell, this will result in emitting the characteristic Kα or Kβ X-rays.

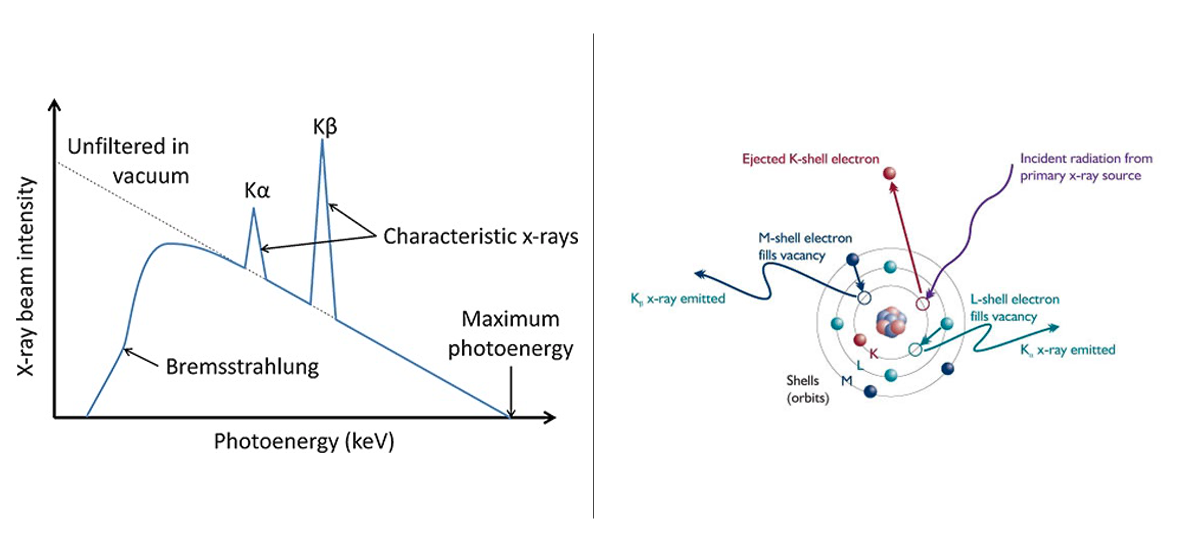
Left: Schematic illustration of characteristic X-ray radiation. Courtesy of museumbulletin.wordpress.com.
Right: X-ray spectra. Courtesy of physicsopenlab.org.

Left: Conventional Lab-Based X-ray Machines: X-ray diffractometer D8 DISCOVER.
Right: The Advanced Photon Source (APS) at the U.S. Department of Energy’s Argonne National Laboratory provides ultra-bright, high-energy storage ring-generated x-ray beams for research in almost all Courtesy of aps.anl.gov. disciplines.

X-ray Scattering from Crystals

Before we learn more about X-ray diffraction methodologies, we need some theoretical background of diffraction. In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions, or molecules in a crystalline material. The smallest group of particles in the material that constitutes this repeating pattern is called the unit cell of the structure. A Bravais lattice represents an infinite array of discrete points, constituting the underlying framework for a crystal structure.

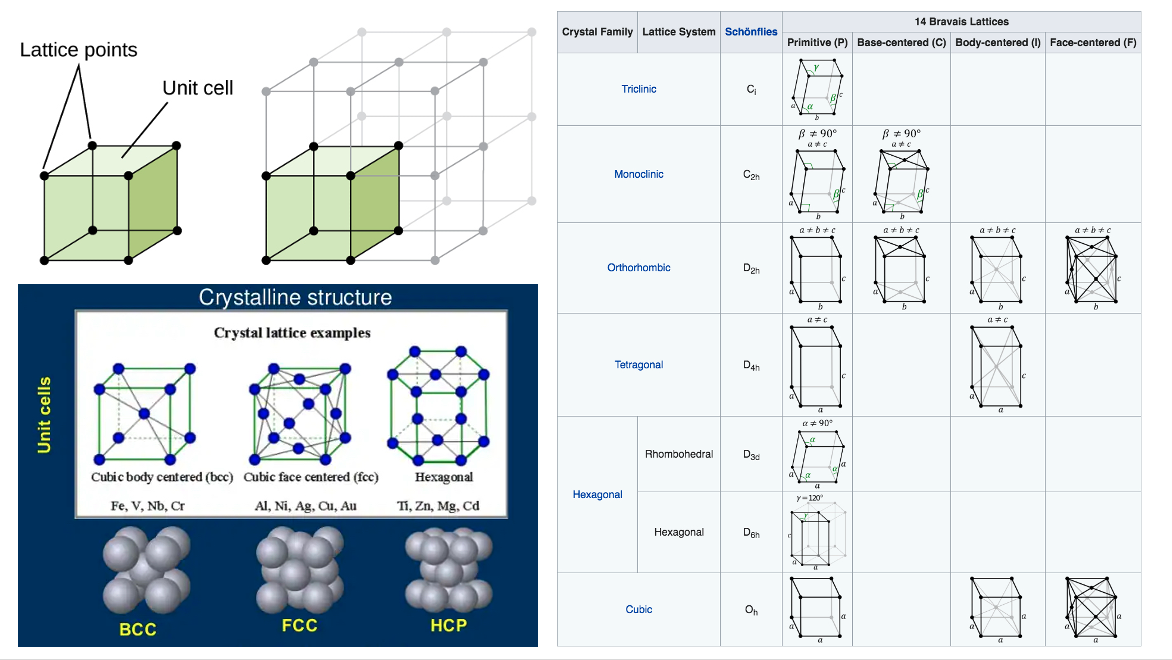
Left: A unit cell shows the locations of lattice points repeating in all directions. Crystal lattice examples. Curtesy of opentextbc.ca.
Right: Two Bravais lattices are considered equivalent if they have the same symmetry elements. In this sense, there are 14 possible distinct Bravais lattices in three-dimensional space, grouped together into 7 more general symmetry categorizations known as lattice systems. Courtesy of docs.exabyte.io.

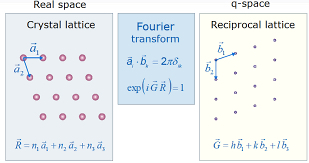
A very important topic in crystallography is the concept of a reciprocal lattice. The reciprocal lattice of the crystal which is also a three dimensional lattice is formed by all the diffraction nodes of various crystallographic planes. It also represents the Fourier transform of other lattice such as Bravais lattice in physics. Normally, the direct space is a periodic spatial function in real-space which is commonly understood as a physical lattice, while the reciprocal lattice exists in reciprocal space (K-space). While this might be counterintuitive to understand, it is a very important mathematical abstraction that is essential for understanding a diffraction pattern of crystalline solids.

Reciprocal Lattice Vectors. Courtesy of teqipiitk.in.

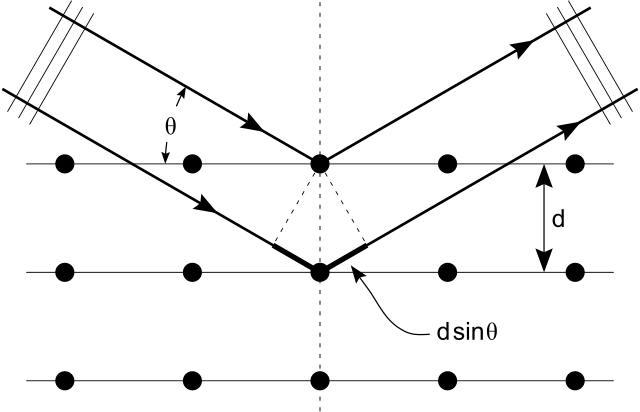
Bragg diffraction from a cubic crystal lattice. Plane waves incident on a crystal lattice at angle θ are partially reflected by successive parallel crystal planes of spacing d. The superposed reflected waves interfere constructively if the Bragg condition nλ = 2dsinθ is satisfied. Courtesy of commons.wikimedia.org.

Ewald Sphere

We can also understand Bragg’s law with the Ewald sphere. It is an imaginary sphere with a radius of λ− 1 in reciprocal space. The center of the Ewald sphere is located at a crystal node to be examined. The incident beam passes through a crystal at the sphere center and targets the origin of the reciprocal lattice located on the surface of the sphere . We can detect diffraction from crystallographic planes when the corresponding reciprocal lattice points touch the Ewald sphere surface. Then these points can form a diffraction pattern. We can also consider placing a polycrystalline solid at the center of Ewald sphere instead. By rotating the reciprocal space in all directions, we can get all the possible crystallographic planes satisfying the Bragg conditions.

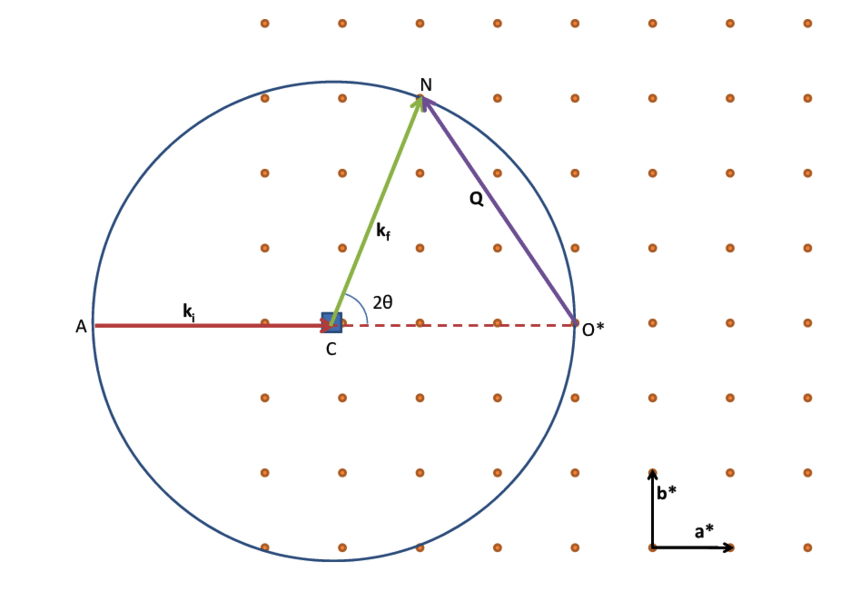
Construction of the Ewald’s sphere in 2D. During a diffraction experiment, the crystal is rotated around its position C. As a result, the reciprocal lattice rotates around its origin O* . Diffraction will occur every time a node of the reciprocal lattice intersects the Ewald’s sphere. Courtesy of researchgate.net.

Now that we learned about the background of crystalline structure, in the next article we will learn more about X-Ray Diffractometry.