Laser-Induced Cavitation and Laser-Fluid Coupling

Introduction and motivation

The development of vapor bubbles in a liquid as a result of laser radiation is known as laser-induced cavitation. These types of bubble formations are observable in microfluidic applications as well. Laser-induced cavitation also happens naturally in a variety of applications when lasers are used to treat materials in a liquid environment.

Examples of this type of processing include liquid-assisted laser surgery, ocular laser surgery, laser angioplasty, and laser lithotripsy. Since it can have both positive and negative impacts, cavitation frequently presents a significant complexity. The effectiveness and safety of these technologies can be increased by better understanding laser-induced cavitation and the ensuing bubble dynamics.

Laser radiation (see Figure 1) can be seen as a preceding event that ends before the vapor (or plasma) bubble begins to expand if the pulse duration is significantly less than the acoustic time scale (i.e., characteristic length divided by the speed of sound in the liquid). In this instance, the analysis of bubble and fluid dynamics and that of laser radiation can be separated.

Bubble dynamics

The dynamics of the bubble may be influenced by both the ongoing phase transition and the initial bubble’s inertia. A non-spherical bubble that reflects the laser beam and profile can be seen in real-world applications as proof of this phenomena.

In this case, the dynamics of the bubble and the surrounding liquid, as well as laser radiation and phase transitions (such as vaporization), should all be examined together as a single system. These models’ analyses often begin with one, two, or more pre-specified bubbles, each with a fixed initial state. This method is no longer viable for bubbles produced by long-pulsed lasers because of the continued laser radiation and phase transition. There hasn’t been a full-domain approach described in the literature that predicts both the two-phase bubble/fluid dynamics and continuous, laser-induced phase transitions.

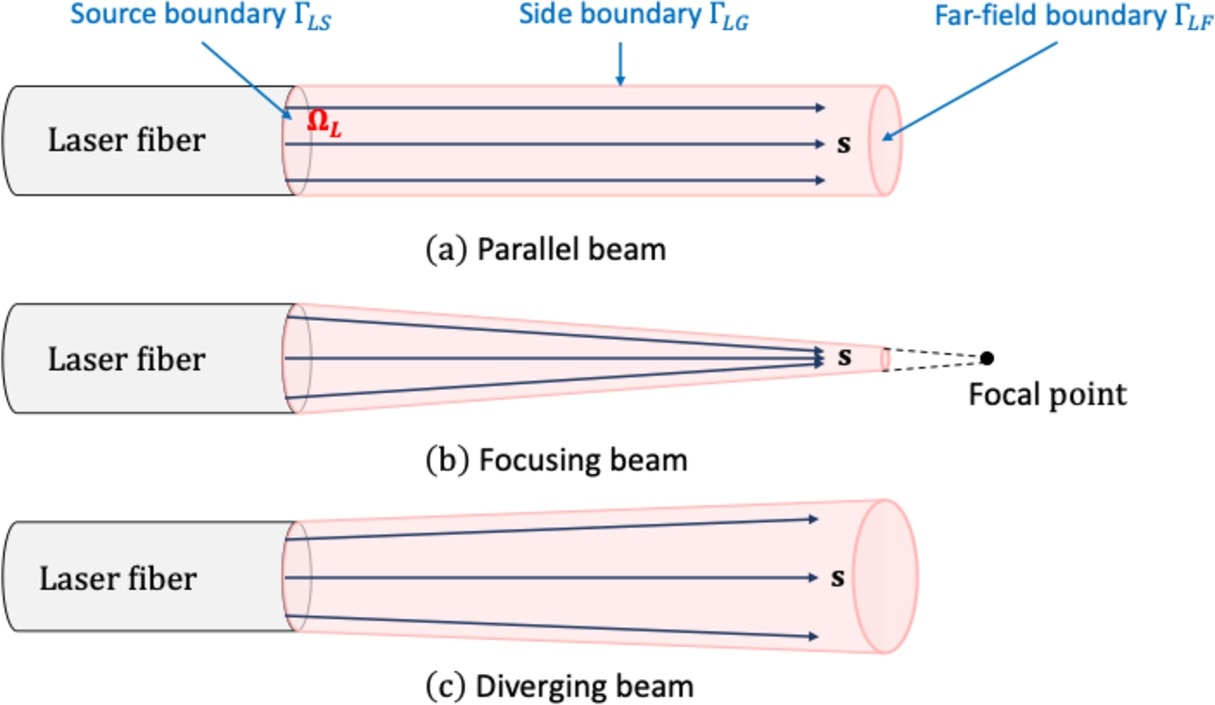
Figure 1: Laser domain geometries; Photo courtesy of Elsevier

Simulation of laser-induced cavitation

Researchers and scientists at Virginia Tech have made an attempt to close that gap. Accordingly, they combine the two-phase Euler equations with an equation for laser radiation that simulates how laser light is absorbed by the two-phase fluid flow. The radiative transfer equation (RTE) is modified to account for the unique characteristics of laser beams (Figure 1), such as monochromaticity, directionality, and a measurable (typically non-zero) focusing or diverging angle, to produce the laser radiation equation (see Figure 2). The coupled fluid-laser system takes into account the laser’s ongoing attenuation by the fluid flow both before and after bubble formation, as well as the impact of temperature variations (Figure 3) and bubble dynamics.

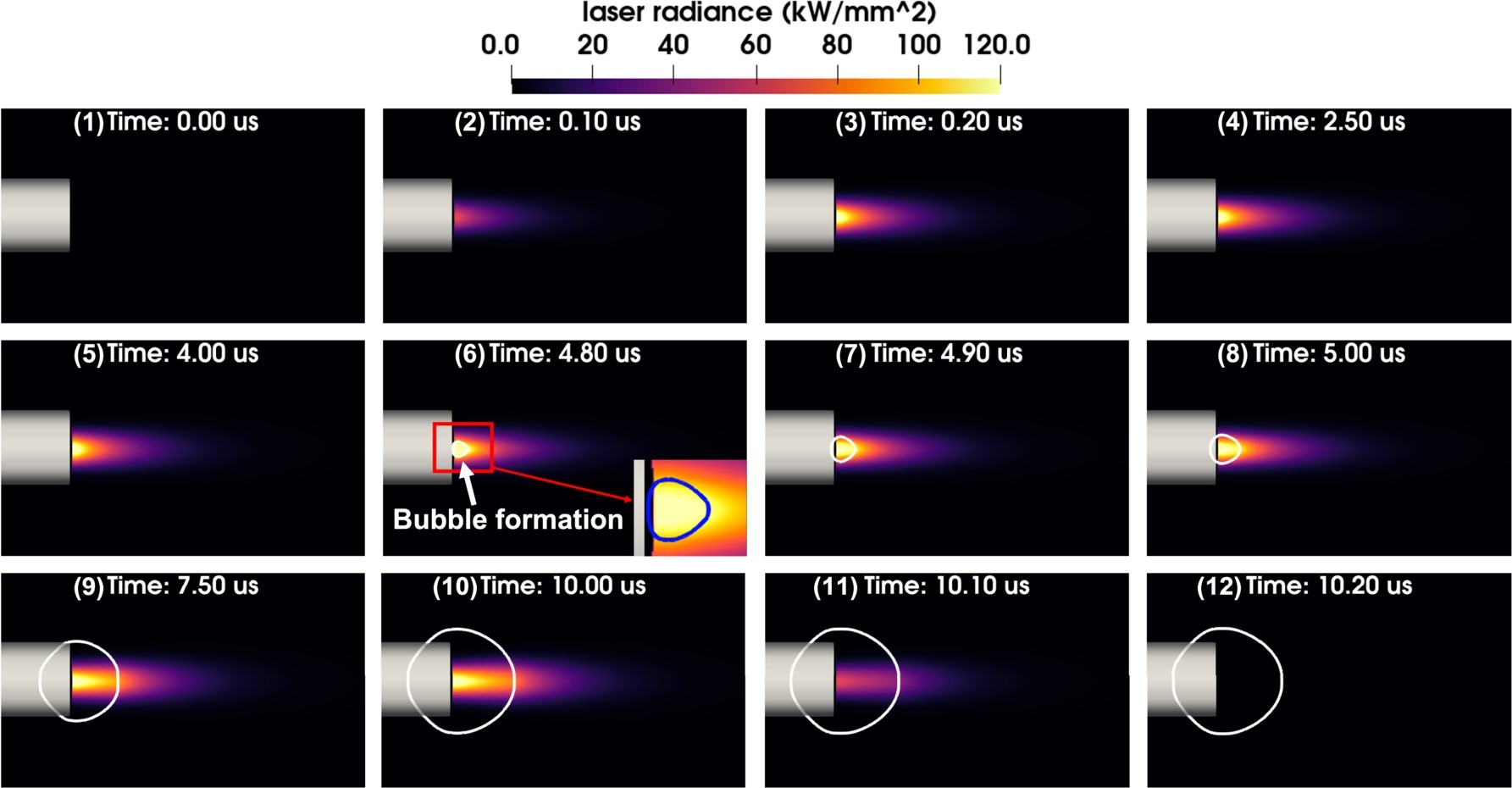
Figure 2: Laser radiance in cavitation induced by a broad beam; Photo courtesy of Elsevier

The researchers at Virginia Tech use an embedded boundary technique to impose the boundary conditions of the laser radiation equation in order to take this complexity into account. Specifically, they employ mirroring and interpolation methods to populate ghost nodes outside the laser domain. This technique, also known as the submerged boundary method or the ghost cell technique, has been used extensively in fluid-structure interaction computations. They provide a technique of latent heat reservoir that takes into account the buildup and release of latent heat in order to capture laser-induced vaporization. The latent heat needed to dissolve the intermolecular interactions is introduced as a new variable for each control volume in the liquid subdomain.

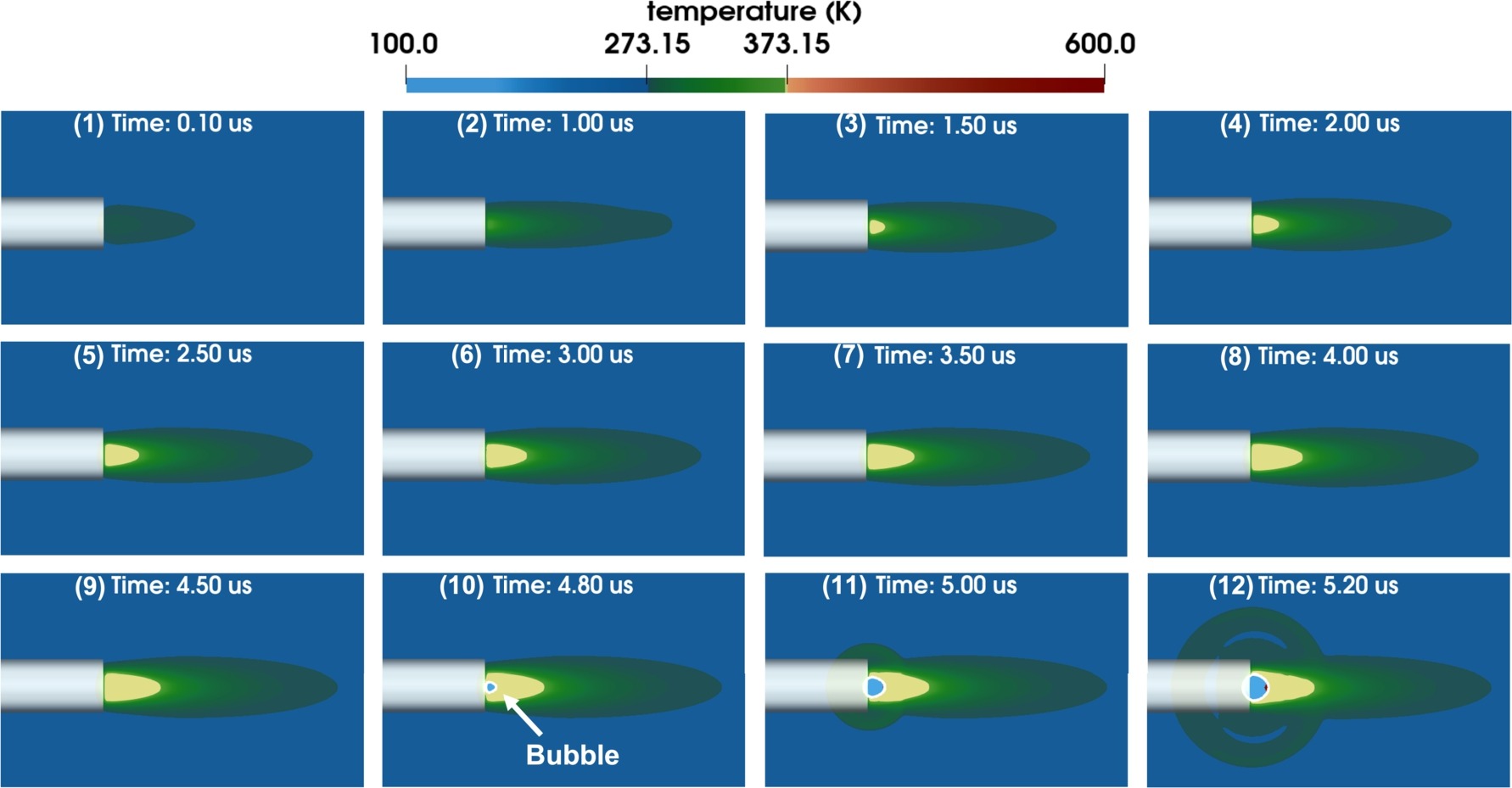
Figure 3: Temperature field in cavitation induced by a broad beam; Photo courtesy of Elsevier

Results of an experiment involving laser-induced cavitation

By converting the equation of state to that of the vapor phase and then adding the latent heat to the enthalpy of the vapor through an isochoric process, the transition from the liquid to the vapor phase is accomplished numerically. The Virginia Tech team uses a localized level set technique to solve the level set equation inside a constrained band containing the liquid-vapor interface in order to track the bubble surface.

The level set approach has been used extensively in the past to follow the development of bubbles that are accelerated by a fluid velocity field (also known as advection). Within control volumes that have recently undergone a phase transition, these researchers change the sign of the level set function value to capture the effect of continual vaporization.

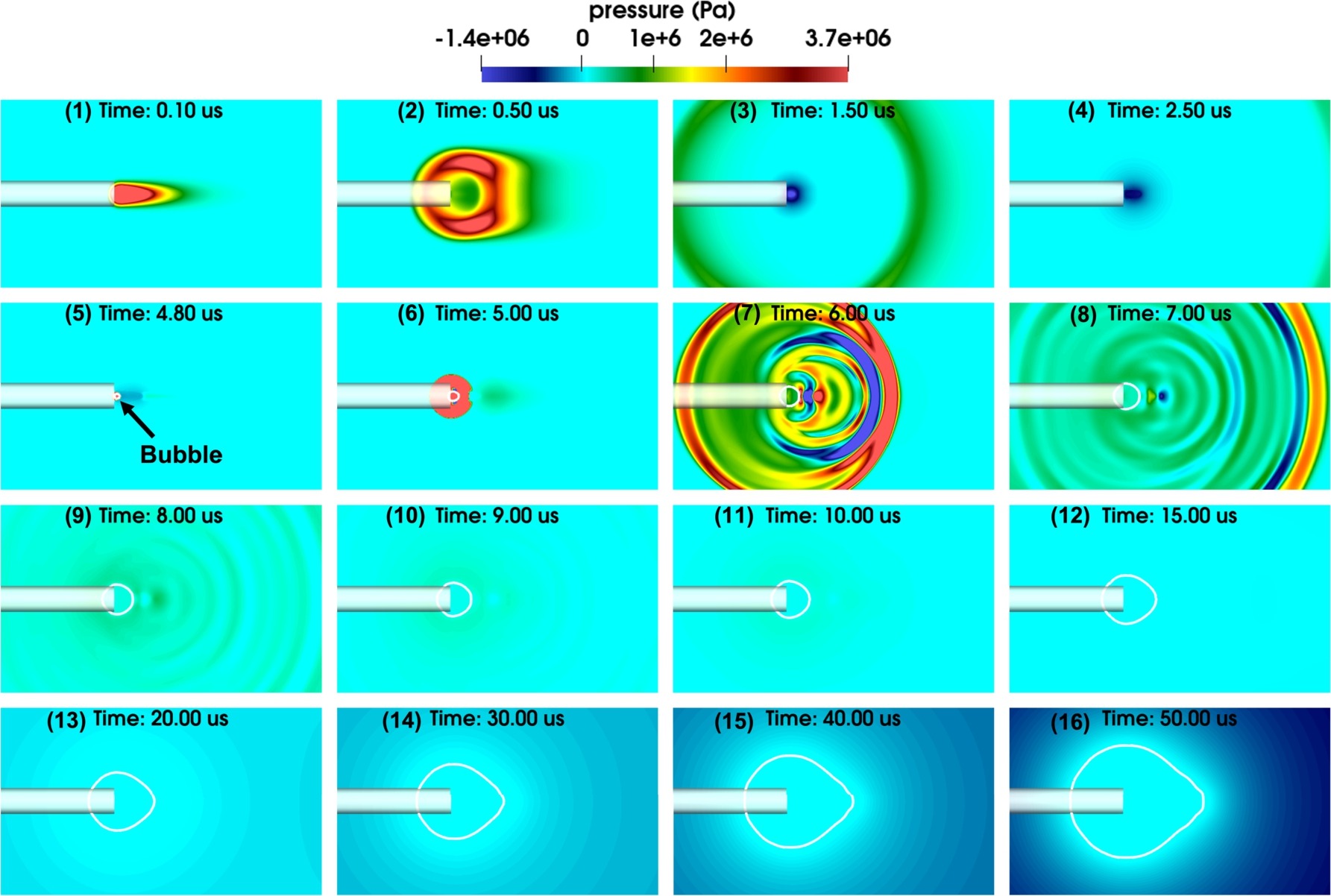
Figure 4: Pressure field in cavitation induced by a broad beam; Photo courtesy of Elsevier

The level set function is then converted back to a signed distance function by solving the level set reinitialization equation. They vary the laser beam width in these simulations to demonstrate that the computational approach is capable of capturing a number of significant phenomena that have been identified in laboratory experiments, such as the formation of a bubble channel that increases the range of laser radiation, also known as the “Moses effect,” non-spherical, beam-dependent bubble expansion, and the emission of acoustic and shock waves (see Figure 4 and Figure 5). This experiment has been also done in a lab (see Figure 6) and the obtained results have been in a good agreement with the numerical results.

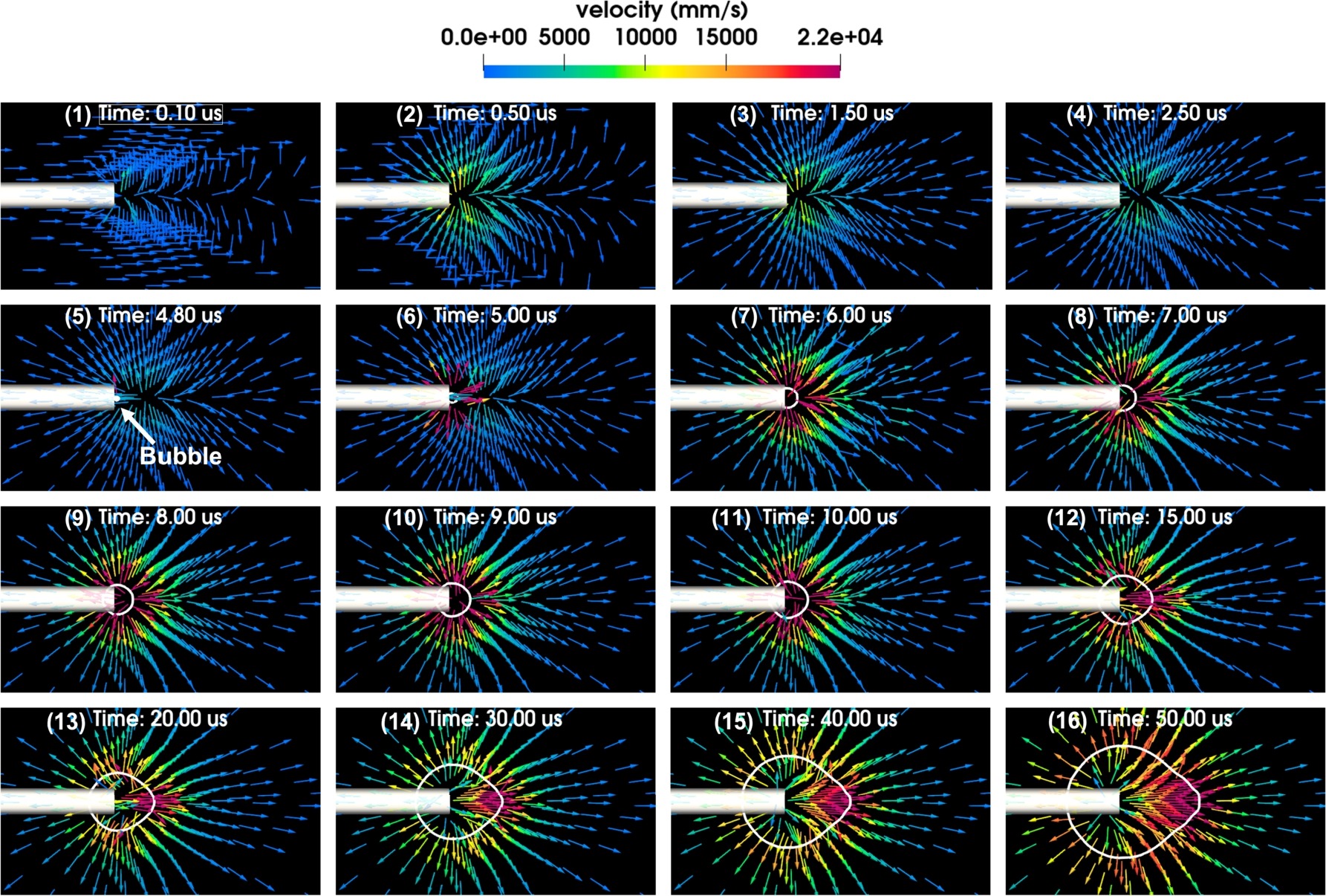
Figure 5: Velocity field in cavitation induced by a broad beam; Photo courtesy of Elsevier

Summary

• The simulation of cavitation caused by long-pulsed laser is done computationally. Varied laser technologies and applications have different definitions of what “long-pulsed” means. It refers to laser pulses in this article that are equal to or longer in duration than the acoustic time scale.
• In this situation, there is a temporal and spatial overlap between the processes of laser radiation, phase transition (i.e. vaporization), and bubble/fluid dynamics. With the aid of a physical model that takes into consideration their interdependencies, the computational technique is intended to replicate these processes simultaneously.
• The fluid dynamics equations and the laser radiation equation are coupled using an embedded boundary approach, enabling the latter to be solved on the same finite volume mesh as the former. In general, the limits of the laser radiation domain cannot be resolved using this mesh.
• The standard level set technique, which takes into account the development and expansion of bubbles as a result of phase transitions, can be seen as an extension of this method. A technique called the latent heat reservoir, which monitors the rise in intermolecular potential energy before phase change, is used to identify local vaporization during simulations.
• It is demonstrated that the computational method can capture a number of significant phenomena in laser-induced cavitation, including non-spherical, beam-dependent bubble expansion, shock waves, and the Moses effect, even with relatively simple material models (see Figure 2, Figure 3, Figure 4, and Figure 5).

Figure 6: A teardrop-shaped vapor bubble observed in laser-induced cavitation; Photo courtesy of Elsevier

This article is brought to you by World Start Tech, a leading manufacturer of lasers and optical sensors.